 Search Here
Search Here
MISC
Parts List
Robot Forum
Chat
Member Pages
Axon MCU
Robot Books
Shop
Contact
SKILLS
How To Build
A Robot
Tutorial
Calculators
Mechanics
Programming
Miscellaneous
Robots
Space
HARDWARE
Actuators
Batteries
Electronics
Materials
Microcontrollers
Sensors
SCIENCE
Robot Journals
Robot Theory
Conferences
|
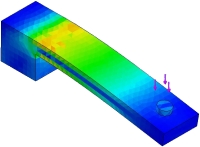
Want to optimize your robot parameters mathematically? Want to verify that an expensive motor you are about to purchase has enough torque? This is a math tutorial for robot chassis construction. This tutorial is useful if you would like to mathematically either prove your robot will work, or optimize it so that it would work better. Better yet, I have one of those degree thingies in Mechanical Engineering so this tutorial should be extra useful . . .
My approach will be talking about the most common calculation uses of mechanical forces for robots. I will offer specific application examples, the theory, equations, and some pretty graphs to help you understand.
Theory: Statics
Statics is concerned about how a mechanical system would act if everything is
perfectly motionless and rigid. It is the most fundamental of all calculations,
and mathematically is no more complicated then highschool algebra. All you need to
understand is how to build an equation from the mechanical parts you use.
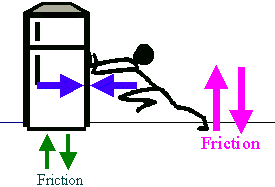
Now suppose you add in friction of joints, efficiency rates, multiple actuators, and unevenly distributed weight across an oddly shaped object. Obviously the problem can balloon to something quite complex. This is what I will talk about, all directly relating to robotics and in simplified form.
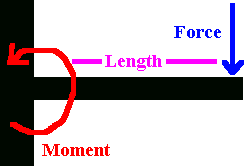
Moment = Force * distance
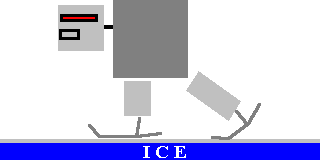
Here is the first example. What you see is an object of some length. It is fixed
rigidly at one end. And the other has some force being applied to it. This force can be
something hanging on it, something pushing it, a hammer hitting it, a gear moving it,
gravity/weight, etc. Does not really matter.
All you do is measure the distance and multiply that by the force that is being applied.
You should always know the expected force being applied to your robot, or you are taking
a risk of buying an actuator that is too weak or too big and strong. If the robot is
lifting a beer can, know the weight of the can. If the robot is climbing, know the estimated
weight of the robot. Even rudimentary calculations can help you better understand
the force requirements of your robot.
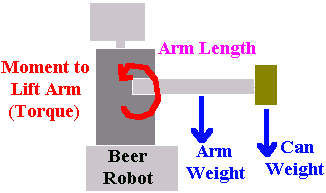
Now suppose your robot is lifting a beer with an arm. A moment about the
shoulder is being created by both the weight of the can,
but also the weight of the robot arm itself. How do you calculate this?
You would add the moments created by each together.
Moment = can_weight * arm_length + arm_weight * 1/2 * arm_length
Notice that for the arm length we only use half the value. Why? Because weight is
distributed throughout the entire arm. Theoretically all you are doing is adding up
all of the force across the arm, and applying it to the center of mass of the
robot arm.
The center of mass is the exact point where an object can be perfectly balanced.
I estimated the center of mass to be the midpoint (1/2 length) of your robot arm.
However it may not be. You can easily find the center of mass of any object by
balancing it on your finger and then measuring that distance with a ruler.
Now suppose you have calculated the moment. What do you do with this number? This
is actually the torque being applied. So when you look for a motor to power
the shoulder of your robot, just reference this calculated value as your minimum required
torque.
The concept of the moment arm can be applied for many different situations.
Sometimes the moment arm can be hidden, so here are a few more examples:
Moment = Torque = Force_A * Pulley_Radius - Force_B * Pulley_Radius
or
Torque = Pulley_Radius * (Force_A - Force_B)
You should also note Force C, the force required to hold the pulley up.
Although this example looks very different from the rest, it is actually exactly
the same.
Both sides of the crowbar create a moment about the pivot point (the triangle tip).
So your equation is this:
Moment Side A = Moment Side B
Force_A * Length_2 = Force_B * Length_1
Now if you knew any three variables out of the four, you can use simple
algebra to calculate the fourth one.
For example, suppose this was a see-saw
at a childrens' playground. Now you have a 40 pound child sitting on one end,
and you plan to catapult him into the next playground. Now this child is
sitting exactly 4 feet from the pivot point. Your plan is to jump on it with
your weight of 200 pounds. What is the closest distance to the pivot point
you can stand on the see-saw and still lift the child into the air?
filling in the equation:
solving:
So what should your factor be? Guess. I would recommend 1.2, but its really
up to you. What does this number mean? Suppose your calculations say you need a motor
rated at least 100Nm, then multiple that by 1.2 to get 120Nm as your minimum motor force.
The factor of safety is not an exact science, obviously. If you expect to have high
fatigue from shock or overuse, high friction, or bending, make the factor of safety higher.
So why not make my safety factor really high? Well, you can, but motors with higher torques
are also more expensive. Thicker robot materials can cost you more too.
So why not a small safety factor? Well, if friction is much higher in your robot
than you expected, your robot just won't work very well.
There is a more scientific method to the safety factor, called statistical analysis.
This involves building then actually testing your robot part under various circumstances until it
breaks. Then statistically (through a histogram) you can determine the optimal properties so it will NEVER break.
However this involves building and breaking a part many times - too much effort for a single robot.
This method is common for car and cell phone manufacturers. Did you know they statistically
determine how many times you can drop a cell phone at any particular angle to make it user proof?
Moment Arms
Moment arms will probably be the most useful for you. The basic equation is moment equals
force times the distance of the beam the force is being applied perpendicularly at.
Pulleys
Calculating pulley forces is very simple. A pulley is a simple moment arm.
The force being applied on the rope multiplied by the pulley radius is
the torque being applied. But now notice that there are two forces countering
each other. This is like two opposite moments, so you would subtract them.
Remember, don't be confused by the device itself. Even if the pulley were square,
the calculation would still be exactly the same. Can you see the moment
arm in this example?
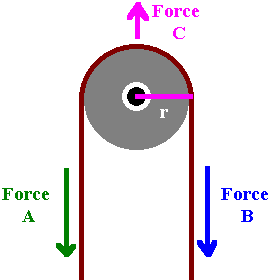
Force C is always Force_A + Force_B + pulley_weight.
Crowbar - Mechanical Advantage Moment Balancing
Another example of a moment would be a crow bar. What you have is a beam, a
pivot point in the center, and a weight on each end. Now suppose you have two
exact same weights. Now move one of those weights real close to the pivot point.
What will happen? The weight that did not move would go down.
Although the force remained the same, the distance
decreased, therefore resulting in a smaller moment.
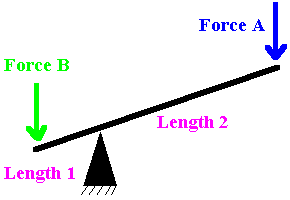
40 lbs * 4 ft = 200 lbs * distance
40 * 4 / 200 = distance = .8 feet
Safety Factor
If you are unsure of various perhaps uncalculatable factors, always add what is called a factor of safety.
For example, suppose you guess a beer can weighs between 1 to 2 pounds. A factor of safety
would say, 'design the system to handle 2.5 pounds, just in case.'
Society of Robots copyright 2005-2014