 Search Here
Search Here
MISC
Parts List
Robot Forum
Chat
Member Pages
Axon MCU
Robot Books
Shop
Contact
SKILLS
How To Build
A Robot
Tutorial
Calculators
Mechanics
Programming
Miscellaneous
Robots
Space
HARDWARE
Actuators
Batteries
Electronics
Materials
Microcontrollers
Sensors
SCIENCE
Robot Journals
Robot Theory
Conferences
Part 3: Computer Vision Algorithms

|
Now that you have learned about biological vision and computer image processing, we now continue on to the basic algorithms of computer vision.
Computer Vision vs Machine Vision
Computer vision and machine vision differ in how images are created and processed. Computer vision
is done with everyday real world video and photography. Machine vision is done in oversimplified situations
as to significantly increase reliability while decreasing cost of equipment and complexity of algorithms.
As such, machine vision is used for robots in factories, while computer vision is more appropriate for robots
that operate in human environments. Machine vision is more rudimentary yet more practical, while
computer vision relates to AI. There is a lesson in this . . .
for each pixel, analyze each of the 8 pixels surrounding it
record the value of the darkest pixel, and the lightest pixel
if (darkest_pixel_value - lightest_pixel_value) > threshold)
What the algorithm does is detect sudden changes in color or lighting, representing
the edge of an object.
Check out the edges on Mona Lisa:
A challenge you may have is choosing a good threshold. This left image
has a threshold thats too low, and the right image has a threshold thats too high.
You will need to run an
image heuristics program
for it to work properly.
You can also do other neat tricks with images, such as thresholding only
a particular color like red.
count the number of continuous edges
if three lines detected, then its a triangle
if four lines, then a square
if one line, then its a circle
by measure angles between lines you can determine more info (rhomboid, equilateral triangle, etc.)
The basic shapes are very easy, but as you get into more complex shapes (pattern recognition) you will have to use
probability analysis. For example, suppose your algorithm needed to recognize between 10 different fruits
(only by shape) such as an apple, an orange, a pear, a cherry, etc. How would you do it?
Well all are circular, but none perfectly circular. And not all apples look the same, either.
By using probability, you can run an analysis that says 'oh, this fruit fits 90% of the characteristics
of an apple, but only 60% the characteristics of an orange, so its more likely an apple.'
Its the computational version of an 'educated guess.' You could also say 'if this particular feature is
present, then it has a 20% higher probability of being an apple.' The feature could be a stem such as on an apple,
fuzziness like on a coconut, or spikes like on a pinneapple, etc. This method is known as feature detection.
To find a blob, you threshold the image by a specific color as shown below. The blue dot represents
the middle mass, or the average location of all pixels of the selected color.
If there is only one blob in a scene, the middle mass is always located in the center of an object.
But what if there were two or more blobs? This is where it fails, as the middle mass is no longer
located on any object:
To solve for this problem, your algorithm needs to label each blob as seperate entities.
To do this, run this algorithm:
if the pixel is a blob color, label it '1'
go to the next pixel
repeat until all pixels are done
What the algorithm does is labels each blob by a number, counting up for every new blob
it encounters. Then to find middle mass, you can just find it for each individual blob.
In this below video, I ran a few algorithms in tandem. First, I removed all non-red objects.
Next, I blurred the video a bit to make blobs more connected. Then, using blob detection,
I only kept the blob that had the most pixels (the largest red object). This removed background
objects such as the fire extinguisher. Lastly, I did center of mass to track the actual
location of the object. I also ran a population threshold algorithm that made the
object edges really sharp. It doesnt improve the algorithm in this case, but it does make
it look nicer as a video.
Feel free to download my custom blob detection RoboRealm file that I used.
In this video, I programmed my ERP to do nothing but middle mass tracking:
This method is clearly useful for picking out the road for road following and obstacles for obstacle avoidance.
Its also used in satellite image processing, such as this image of a city (yellow/red for buildings), forest (green), and river (blue):
If Greenpeace wanted to know how much forest has been cut down, a simple pixel density count can be done.
To do this, simply count and compare the forest pixels from before and after the logging.
A major benefit to this bottom-up method to image processing is its immunity to heavy image noise.
Blobs do not need to be identified first. By finding the middle mass of these pixels, the center location
of each object can be found.
Need an algorithm to identify roads for your driving robot?
This below video (from my house front door) is an example of me simply maximizing RBG (red blue green) colors. Pixels
that are more blue than any other color become all blue, pixels more green than any other color
become all green, and the same for red. What you get is the road being all blue, the grass
being all green, and houses being red. Its not perfect, yet still works amazingly well
for a simple pixel classification algorithm.
This algorithm would well compliment another algorithm(s).
Feel free to download my custom pixel classification RoboRealm file that I used.
In this example, various features of an adorably cute squirrel (its the species name) are obtained
for comparison with other objects.
This method is also used for feature detection (mentioned earlier) and facial recognition . . .
Here is an excercise for you. Suppose you have a friend coming to your family's house and she/he wants
to recognize every face by name before arriving.
If you could only give a written list of facial features of each family member, what would you say about each face?
You might describe hair color, length, or style. Maybe your sister has a beard. One person might
have a more rounded face, while another person might have a very thin face. For a family of 4 people
this excercise is really easy.
But what if you had to do it for everyone in your class? You might
also analyze skin tone, eye color, wrinkles, mouth size . . . the list goes on. As the number of people
that will be analyzed grows, so would the number of required descriptions for each face.
One popular way of digitizing faces is to measure the distance between each eye, size of the head,
distance between eyes and mouth, and length of mouth. By keeping a database of these values,
surprisingly you can accurately identify thousands of different faces. Hint: notice how the features
on Mona Lisa's face above is much easier to identify and locate after edge detection.
Unfortunately for law enforcement this method does not work outside of the lab. This is because
it requires facial images that are really close and clear for the measurements to be done accurately.
It is also difficult to control which way a person is looking, too. For example, can you make out the
facial measurements of the man in this security cam image?
Have a look at this below image. Despite these pictures also being tiny and blurry, you can somehow recognize
many of them! The human brain obviously has other yet undiscovered methods of facial recognition . . .
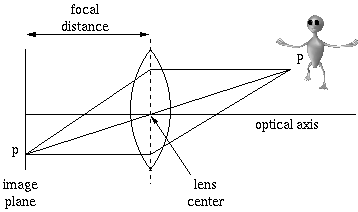
First lets analyze the robot camera itself. Although a simplification resulting in minor error,
the pinhole camera model will be used in the following examples:
The image plane is where the photo-receptors are located in the camera, and the lens
is the lens of the camera. The focal distance is the distance between
the lens and the photo-receptors (can be found in the camera datasheet).
Point P is the location of the alien, and point p is where the alien
appears on the photo-receptors. The optical axis is the direction the camera is pointing.
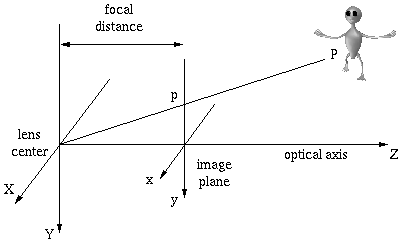
Redrawing the diagram to make it mathematically simpler to understand,
we get this new diagram
with the following equations for a single camera:
CASE 1: Parallel Cameras
The Z-axis is the optical axis (the direction the cameras are pointing). b is
the distance between cameras, while f is still the focal length.
The equations of stereo triangulation (because it looks like a triangle) are:
CASE 2a: Non-Parallel Cameras, Rotation About Y-axis
calculating for the alien location . . .
CASE 2b: Non-Parallel Cameras, Rotation About X-axis
CASE 2c: Non-Parallel Cameras, Rotation About Z-axis
Please continue on in the Computer Vision Tutorial Series
for Part 4: Computer Vision Algorithms for Motion.
Edge Detection
Edge detection is a technique to locate the edges of objects in the scene. This can be useful for locating the horizon,
the corner of an object, white line following, or for determing the shape of an object. The algorithm is quite simple:
sort through the image matrix pixel by pixel
then rewrite that pixel as 1;
else rewrite that pixel as 0;




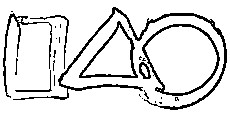
Shape Detection and Pattern Recognition
Shape detection requires preprogramming in a mathematical representation database of the shapes you wish to detect.
For example, suppose you are writing a program that can distinguish between a triangle, a square,
and a circle. This is how you would do it:
run edge detection to find the border line of each shape
a sharp change in line direction signifies a different line
do this by determining the average vector between adjacent pixels


Middle Mass and Blob Detection
Blob detection is an algorithm used to determine if a group of connecting pixels are related to each other.
This is useful for identifying seperate objects in a scene, or counting the number of objects in a scene.
Blob detection would be useful for counting people in an airport lobby, or fish passing by a camera.
Middle mass would be useful for a baseball catching robot, or a line following robot.



go through each pixel in the array:
otherwise label it 0
if it is also a blob color
and if it is adjacent to blob 1
label it '1'
else label it '2' (or more)
Pixel Classification
Pixel Classification is when you assign each pixel in an image to an object class.
For example, all greenish pixels would be grass, all blueish pixels would be sky or water,
all greyish pixels would be road, and all yellow would be a road lane divider.
There are other ways to classify each pixel, but color is typically the easiest.
![]()
Image Correlation (Template Matching)
Image correlation is one of the many forms of template matching for simple object recognition.
This method works by keeping a large database of various imaged features, and computing 'intensity similiarity' of an
entire image or window with another.

Facial Recognition
Facial recognition is a more advanced type of pattern recognition. With shape recognition
you only need a small database of mathematical representations of shapes. But while basic shapes like a
triangle can be easily described, how do you mathematically represent a face?




Stereo Vision
Stereo vision is a method of determing the 3D location of objects in a scene by comparing
images of two seperate cameras. Now suppose you have some robot on Mars and he sees an alien
(at point P(X,Y)) with two video cameras. Where does the robot need to drive to run over this alien
(for 20 kill points)?

x_camL = focal_length * X_actual / Z_actual
y_camL = focal_length * Y_actual / Z_actual
Now moving on to two parallel facing cameras (L for left camera and R for right camera), we have this diagram:
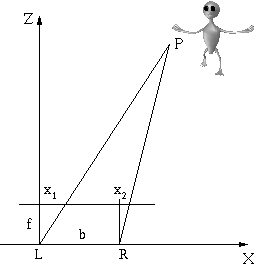
Z_actual = (b * focal_length) / (x_camL - x_camR)
X_actual = x_camL * Z_actual / focal_length
Y_actual = y_camL * Z_actual / focal_length
And lastly, what if the cameras are pointing in different non-parallel directions? In this below diagram,
the Z-axis is the optical axis for the left camera, while the Zo-axis is the optical axis of the right camera.
Both cameras lie on the XZ plane, but the right camera is rotated by some angle phi. The point
where both optical axes (plural for axis, pronounced ACKS - I) intersect at the point (0,0,Zo) is called the fixation point.
Note that the fixation point could also be behind the cameras when Zo < 0.
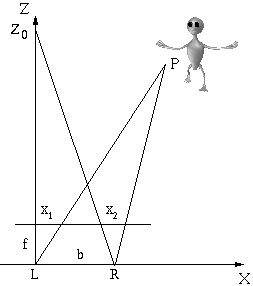
Zo = b / tan(phi)
Z_actual = (b * focal_length) / (x_camL - x_camR + focal_length * b / Zo)
X_actual = x_camL * Z_actual / focal_length
Y_actual = y_camL * Z_actual / focal_length
calculating for the alien location . . .
Z_actual = (b * focal_length) / (x1 - x2)
X_actual = x_camL * Z_actual / focal_length
Y_actual = y_camL * Z_actual / focal_length + tan(phi) * Z
For simplicity, rotation around the optical axis is usually dealt with by rotating the image before applying matching and triangulation.
Given the translation vector T and rotation matrix R describing the transormation from
left camera to right camera coordinates, the equation to solve for stereo triangulation is:
p' = RT ( p - T )
where p and p' are the coordinates of P in the left and right camera coordinates respectively, and RT is the transpose (or the inverse) matrix of R.
Society of Robots copyright 2005-2014